[nowcoder2] 补题向
A.run
题意
白云可以跑$k$米或者走$1$米,但不能连续跑,问到达终点有多少种方案。
题解
1步2步上楼梯的加强版。典型的dp题。
- $dp[i][0/1]$表示第$i$米最终是走还是跑的方案数
转移方程
- $dp[i][0] = dp[i-1][1]+dp[i-1][0]$
- $dp[i][1] = dp[i-1][0]$
AC代码
1 |
|
D.Money
题意
白云可以在一个商店里卖或者买商品,但白云只能带一个商品。问最多能赚多少钱在最少的交易下。
题解
dp
$dp[i][0]$表示在$i$最后一次交易是买入的最优值,$dp[i][1]$表示在$i$最后一次交易是卖出的最优值。转移方程。
- 在$[1,i-1]$中卖出的最优值后在$i$买入或者不买入中取最好值。$dp[i][0]=max(dp[i-1][0],dp[i-1][1]-a[i])$
- 在$[1,i-1]$买入的最优值后在$i$卖出或者不卖中取最大值。$dp[i][1] = max(dp[i-1][1],dp[i-1][1]+a[i])$
只有由于要求最小交易次数,用pair<ll,int>来表示,第一个是金钱,第二个是交易次数,求最小次数,所以用min,并且把金钱变成负值,就可以相当于反向取最大了。
AC代码copydls的
1 |
|
贪心做法
1 |
|
G transform
题意
白云要把一个数轴上的箱子中的产品搬到一个箱子点上,每个箱子都有一个价值,每次搬一个产品从箱子$a$到$b$上都要花费$2*abs(x[a]-x[b])$的力气,问在$T$总力气下,可以获得多少价值。
题解
二分+前缀数组
首先我们可以确定放箱子肯定是选择一定的区间内,因为每搬一个产品,肯定是越近消耗得越好,区间中只有左端点和右端点可能没搬完。
区间中,把所有产品集中到产品中位数,即改点左边的产品和右边的产品数量接近一致。便体力消耗最小。
难点
对于前缀数组的处理,我们用$suma$表示前缀产品和,$sumt$表示前缀对于假设运送产品到0点的和。$sumt[r]-sumt[l-1]$表示$[l,r]$移动到0点所需要的力气。
- 那么如果我们将产品$[l,r]$运送到点$l$的消耗相当于把$[l,r]$中的元素都先运送到$l$中之后再把$l$中的元素送到0,进行减一哈,就是答案。$ans = sumt[r]-sumt[l-1]-(suma[r]-suma[l-1])*x[l]$
- 将产品$[l,r]$运送到$r$点,相当于我们先把$[l,r]$转移到$r$上面之后再统一移动到0点。$ans+sumt[r]-sumr[l-1]=(suma[r]-suma[l-1])*x[r]$。
之后枚举每个$l$的每个$r$和每个$r$的每个$l$,枚举的时候固定$l$或者$r$是消耗完全的。
二分又一个小套路。
1 | int l,r,mid,ans; |
AC代码
1 |
|
https://www.nowcoder.com/discuss/88268?type=101&order=1&pos=4&page=1
H.travel
题意
给定一棵树,树上每个点有一个$val$,从树上走三次,不能走重复的点,问能获得的最大价值是多少。
题解
树形dp
$f[i][j]$表示以$i$为根的子树选了$j$条路径的最大权值和。(也是包含$i$点)
$g[i][j]$表示以$i$为根的子树选了$j$条路径加上一条包含$i$到根节点链的最大权值。
根据题意可以知道,如果我们$i$是竖直链,那么加入一个没有竖直链的。
- $g[u][i] = max(g[u][i],f[v][x]+g[u][i-x])$
- $g[u][i] = max(g[u][i],g[v][x]+f[v][i-x])$
如果$i$不是竖直链
- $f[u][i]=max(f[u][i],f[v][x]+f[u][i-x])$
对不起,我编不下去了。就是瞎几把转移转移。能转移的状态就都转移了就行了。
AC代码
1 |
|
1 | //dls队伍代码,感觉比标程的容易懂一点。 |
I.Car
题意
给定一个长度为$n$的正方形,在上面放车。车有如下性质
- 速度一样
- 不能改变方向
- 起点都在矩阵的边缘
题解
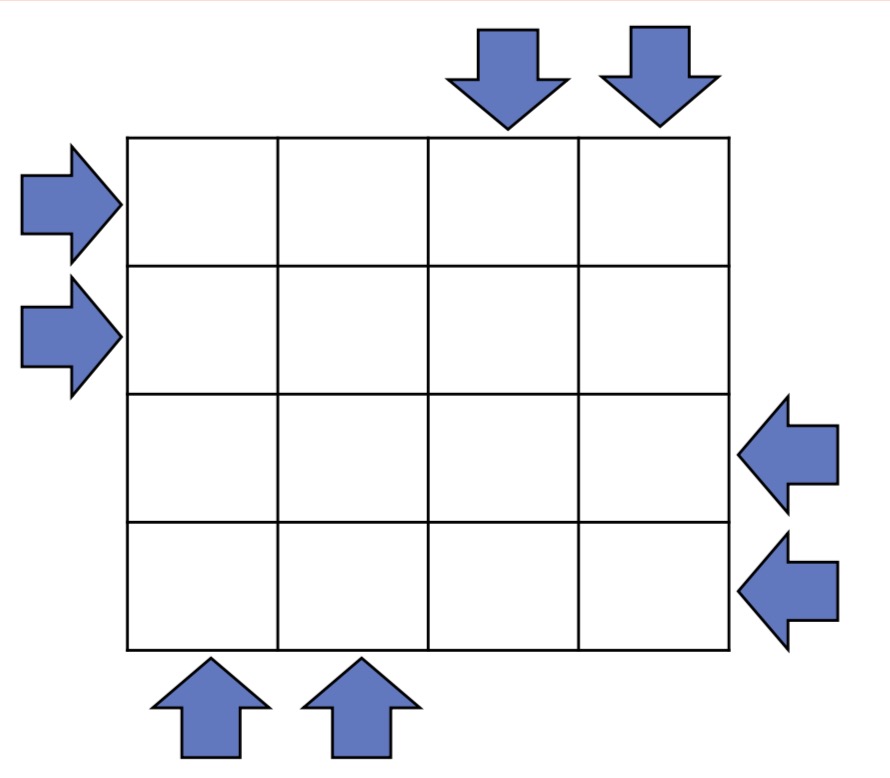
奇数点特判一下,免得减了两次。题解也是经验所得,莫得证明。
AC代码
1 |
|
J.Farm
题意
有一块$nm$的田,里面每一个土地都种$a[i][j]$的植物,每一种植物都有专属化肥,如果用错化肥就挂了。问在进行$T$次区间浇化肥后,挂了过多少个植物。
题解
我一开始想的是能不能统计一下前缀和,如果加入的肥料和是植物种类的倍数就是对的。但是需要随机算法,避免出题人卡。毕竟是假算法。还是乖乖按照标答思路来。。
将化肥按照二进制分为肯定对植物不好和可能对植物好。如
$a$植物代号是101010,那么检查每一位的时候,101011肯定对它不好,101110在检查前几位的时候可能对它好。
分辨植物是否死亡就看。
- 他加入对它好的次数是不是总的施在他身上的次数。如果不等,说明有其他不好的施肥了,那他就挂了。
- 他加入对它不好的次数存不存在,如果有,那他也挂了。
还有一个细节,定义数组更加环保和不可能爆空间。之后可以定义
1 | int f[maxn]; |
还有一个细节就是前缀和你如果想要改变一个区间的前缀和,那就
1 | void add(int x1,int x2,int y1,int y2){ |
AC代码
1 |
|
偷窥到大佬还有用树状数组做的。先copy一下代码。
1 |
|
